CADENA DE MARKOV
La base de las cadenas es la conocida como propiedad de Markov, la cual resume lo dicho anteriormente en la siguiente regla: lo que la cadena experimente en un momento t + 1 solamente depende de lo acontecido en el momento t (el inmediatamente anterior).
Dada esta sencilla explicación de la teoría, puede observarse que es posible a través de la misma conocer la probabilidad de que un estado ocurra en el largo plazo. Esto ayuda indudablemente a la predicción y estimación en largos periodos de tiempo.
¿Dónde se utiliza la cadena de Markov?
Las cadenas de Markov han experimentado una importante aplicación real en el ámbito de los negocios y las finanzas. Esto, al permitir, como se ha señalado, analizar y estimar futuros patrones de conducta de los individuos atendiendo a la experiencia y los resultados anteriores.
Lo anterior puede reflejarse en diferentes campos como la morosidad, el estudio de las conductas de consumidores, la demanda estacional de mano de obra, entre otros.
El sistema elaborado por Markov es bastante sencillo y cuenta, como hemos dicho, con una aplicación práctica bastante fácil. Sin embargo, muchas voces críticas señalan que un modelo tan simplificado no puede ser totalmente efectivo en procesos complejos.
Ejemplos:
- Una empresa esta considerando utilizar Cadenas de Markov para analizar los cambios en las preferencias de los usuarios por tres marcas distintas de un determinado producto. El estudio ha arrojado la siguiente estimación de la matriz de probabilidades de cambiarse de una marca a otra cada mes:
En primer lugar definimos la variable aleatoria que representa la marca que adquiere un cliente cualquiera en el mes n. Dicha variable aleatoria puede adoptar los valores 1,2,3 en el mes n=0,1,2,3,..
Adicionalmente conocemos cuál es la distribución inicial y la matriz de probabilidades de transición en una etapa tal como se observa a continuación:
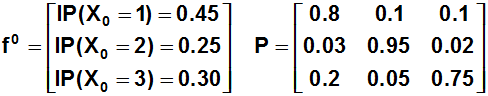
Luego para conocer la distribución de las participaciones de mercado al cabo de 2 meses (2 etapas) podemos utilizar la fórmula :
¿Cuál es la probabilidad que un paciente en estado crítico un día Jueves esté estable el día Sábado?.
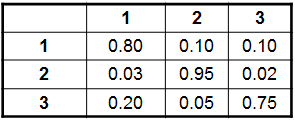
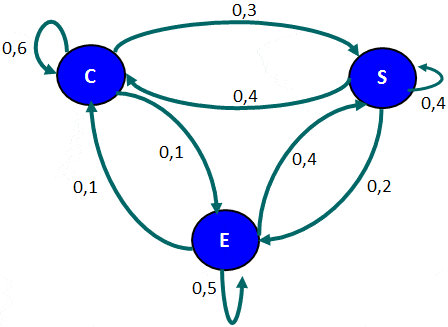
Sea la variable aleatoria que indica el estado que se encuentra un paciente cualquiera en el hospital en el día n. Los valores posibles para dicha variable son C, S y E, representando los estados crítico, serio y estable, respectivamente. Un grafo que representa dicho proceso estocástico dada la tabla anterior es:
Notar que de forma equivalente se pueden utilizar las ecuaciones matriciales :
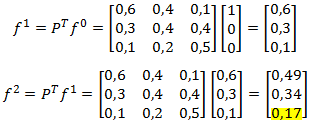
Se comprueba que la probabilidad de pasar del estado crítico al estado estable al cabo de 2 etapas es de un 17%.
En este caso cambia la distribución inicial respecto al escenario anterior (ahora el paciente está en estado estable), no obstante, también resulta de nuestro interés analizar qué sucede al cabo de 2 etapas.
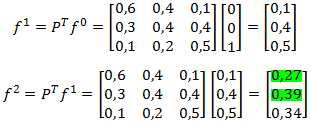
Con color verde se marca la probabilidad de que comenzando en un estado estable al cabo de 2 días un paciente se encuentre en estado crítico o serio. La suma de dichas probabilidades es un 66% que da respuesta a la interrogante anterior.
¿Qué porcentaje de la Unidad de Cuidados Intensivos usted diseñaría y equiparía para pacientes en estado crítico?.
Naturalmente se desea estimar la probabilidades de estado en el largo plazo independiente de la distribución inicial. La cadena es irreducible con estados recurrentes positivos aperiódicos. Utilizando las ecuaciones de estado estable presentadas en el Ejercicio N°2 se obtiene que ,
y
, que representan la probabilidad de que un individuo se encuentre en estado crítico, serio y estable, respectivamente.

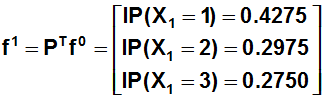
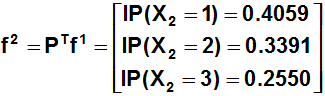

No hay comentarios:
Publicar un comentario