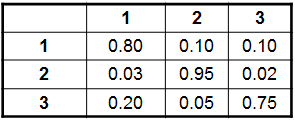
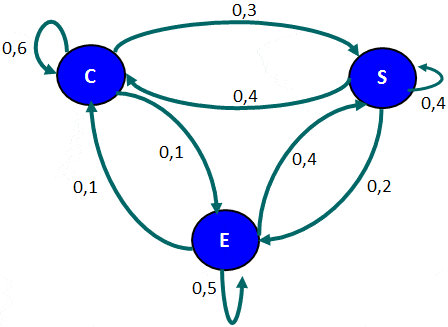
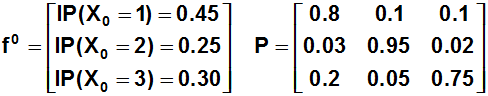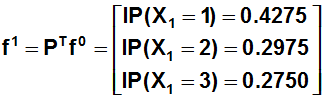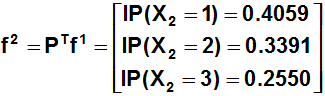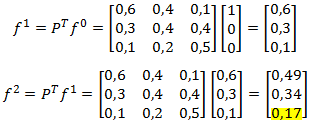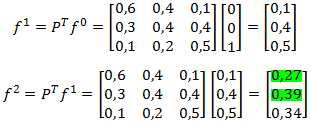martes, 31 de mayo de 2022

 Arboles de Decisión

Un árbol de decisión es una especie de mapa en que se muestra cada una de las opciones de decisión posibles y sus resultados. Este es tremendamente útil para aquellas personas que tienen que tomar decisiones en un negocio, ya que te permite comparar diferentes decisiones y acciones según sus costos, probabilidades y beneficios.

Ejemplos:

El grupo de diseño del producto de Flores Electric Supplies, Inc., ha determinado que necesita diseñar una nueva serie de interruptores. Debe decidirse por una de las tres estrategias de diseño. El pronóstico del mercado es para 200,000 unidades. Cuanto mejor y más sofisticada sea la estrategia de diseño y mayor el tiempo invertido en ingeniería de valor, menor será el costo variable.

El jefe de ingeniería de diseño, Dr. W. L. Berry, decidió que los siguientes costos son una buena estimación de los costos iniciales y variables relacionados con cada una de las tres estrategias:

  1. Baja tecnología: proceso con poca tecnología y bajo costo que consiste en contratar a nuevos ingenieros con poca experiencia. Esta posibilidad tiene un costo de $45,000 y probabilidades de costo variable de 0.3 para $0.55 cada uno, 0.4 para $0.50, y .3 para $0.45.
  2. Subcontrato: enfoque de mediano costo que emplea un buen equipo de diseño externo. Esta alternativa tendría un costo inicial de $65,000 y probabilidades de costo variable de 0.7 para $0.45 cada uno, 0.2 para $0.40, y 0.1 para $0.35.
  3. Alta tecnología: enfoque de alta tecnología en el que se usa lo mejor del personal interno y la más moderna tecnología de diseño asistido por computadora. Esta alternativa tiene un costo inicial de $75,000 y probabilidades de costo variable de 0.9 para $.40 y 0.1 para $0.35.

¿Cuál es la mejor decisión con base en un criterio de valor monetario esperado (VME)? (Nota: Queremos el VME más bajo puesto que se manejan costos en este problema).

Elaboramos el árbol de decisión según las opciones que nos muestra el problema:

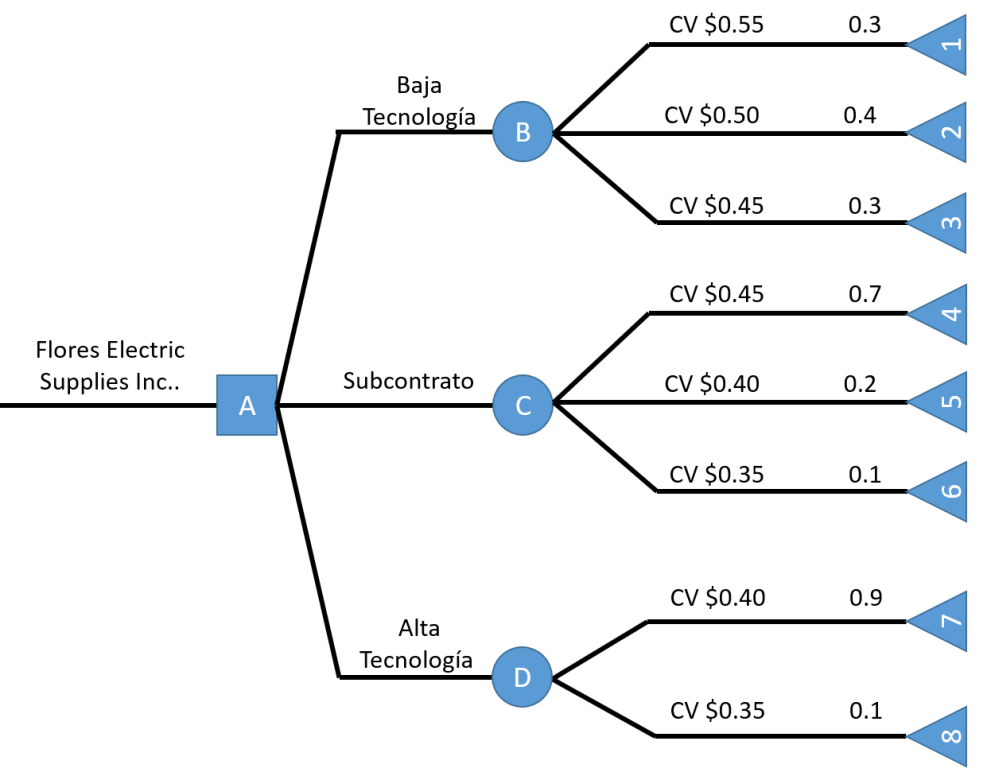
Ejercicios resueltos de árbol de decisiones

CV = Costo Variable

Procedemos a calcular los extremos de los nodos de nuestro árbol:

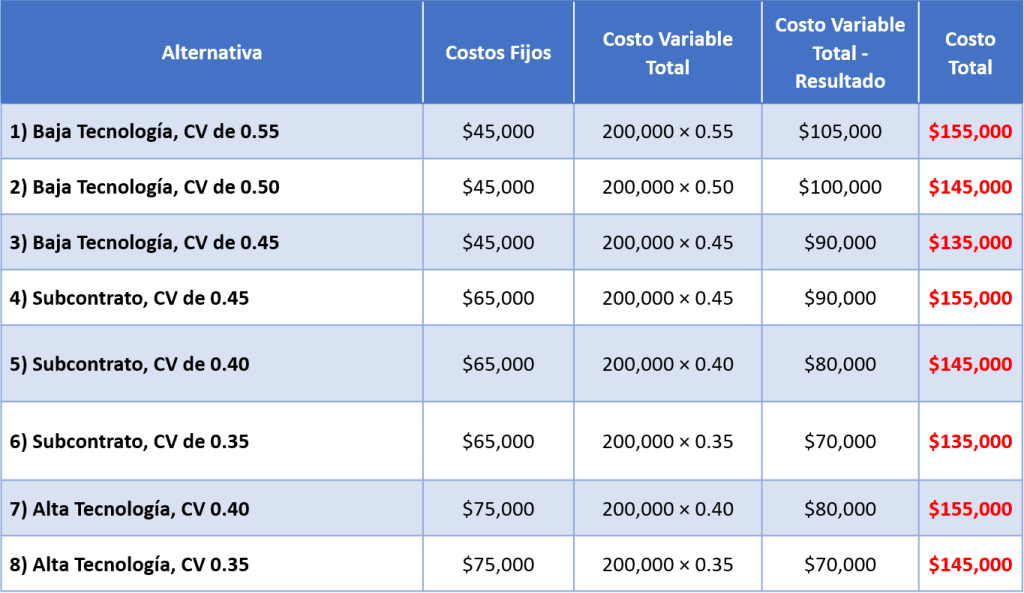
Ejercicios resueltos de árbol de decisiones

El costo total se obtiene sumando el costo fijo mas el costo variable total; teniendo en cuenta el pronóstico del mercado de 200,000 unidades.

Finalmente calculamos los valores de los nodos intermedios y marcamos con 2 líneas las alternativas rechazadas.

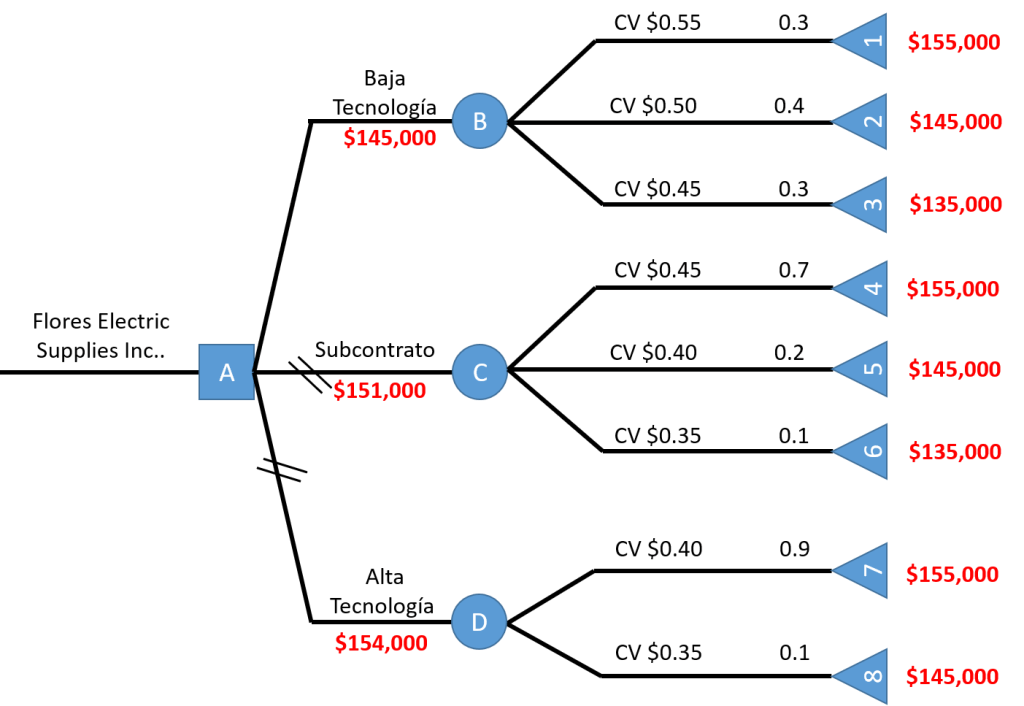
Ejercicios resueltos de árbol de decisiones

Como evaluamos el costo total de las estrategias que evalúa la empresa; elegiremos la alternativa con valor monetario esperado: Baja Tecnología.



2. Un gerente está tratando de decidir si debe comprar una máquina o dos. Si compra sólo una y la demanda resulta ser excesiva, podría adquirir después la segunda máquina. Sin embargo, perdería algunas ventas porque el tiempo que implica la fabricación de este tipo de máquinas es de seis meses. Además, el costo por máquina sería más bajo si comprara las dos al mismo tiempo. La probabilidad de que la demanda sea baja se ha estimado en 0.30. El valor presente neto, después de impuestos, de los beneficios derivados de comprar las dos máquinas a la vez es de $90,000 si la demanda es baja, y de $170,000 si la demanda es alta.

Si se decide comprar una máquina y la demanda resulta ser baja, el valor presente neto sería de $120,000. Si la demanda es alta, el gerente tendrá tres opciones. La de no hacer nada tiene un valor presente neto de $120,000; la opción de subcontratar, $140,000; y la de comprar la segunda máquina, $130,000.

  1. Dibuje un árbol de decisiones para este problema.
  2. ¿Cuántas máquinas debe comprar la compañía inicialmente? ¿Cuál es el beneficio esperado de esta alternativa?

Elaboramos el árbol de decisión según las opciones que nos muestra el problema:

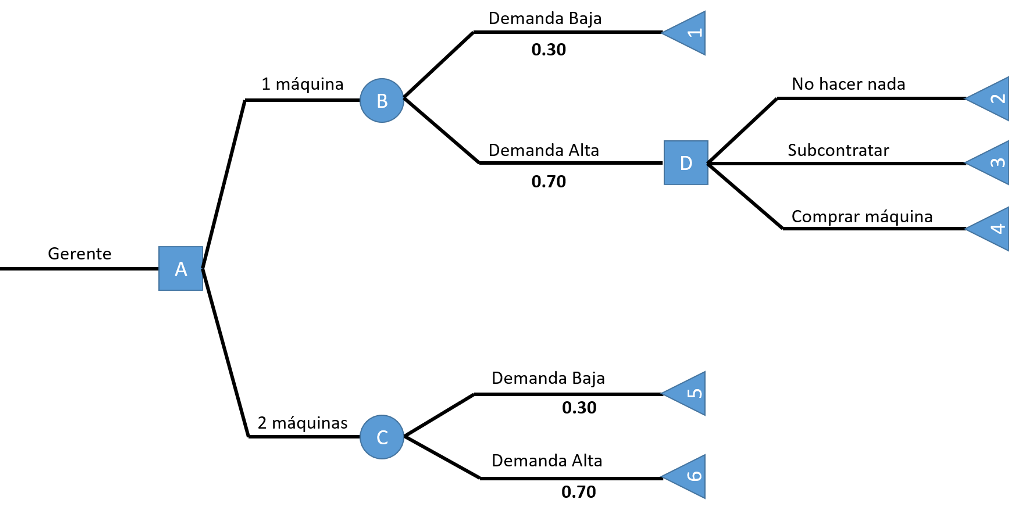
Ejercicios resueltos de árbol de decisiones

Procedemos a calcular los extremos de los nodos de nuestro árbol:

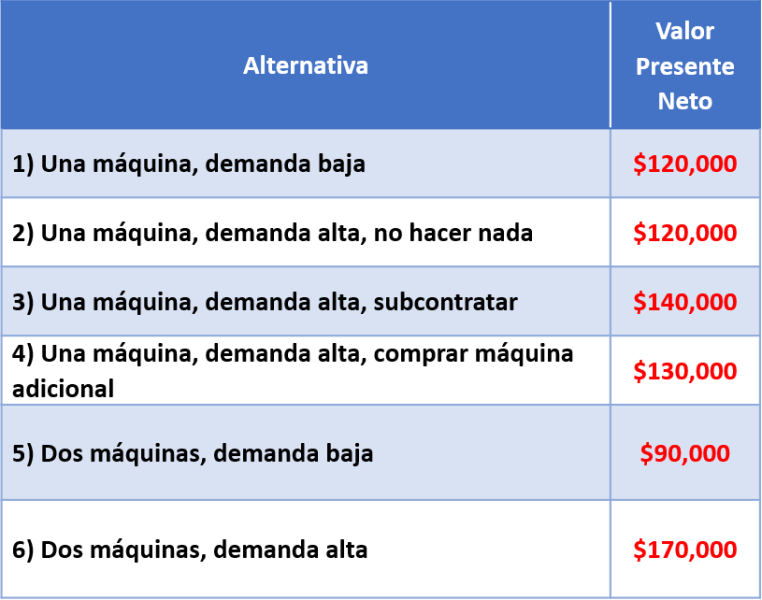
Ejercicios resueltos de árbol de decisiones

Finalmente calculamos los valores de los nodos intermedios y marcamos con 2 líneas las alternativas rechazadas; quedando nuestro árbol de la siguiente manera:

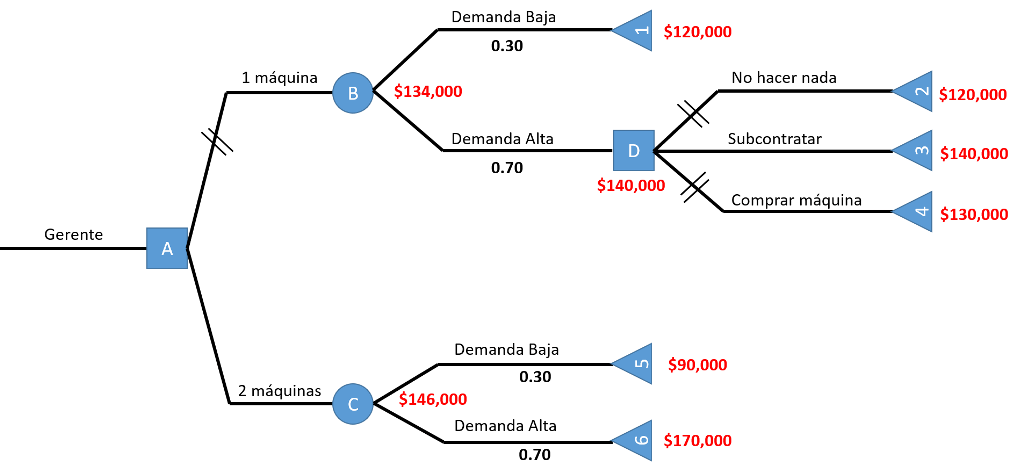
Ejercicios resueltos de árbol de decisiones

La compañía debe comprar dos máquinas   que representa un beneficio esperado de $146,000.

en No hay comentarios:

 CADENA DE MARKOV 

La cadena de Markov, también conocida como modelo de Markov o proceso de Markov, es un concepto desarrollado dentro de la teoría de la probabilidad y la estadística que establece una fuerte dependencia entre un evento y otro suceso anterior. Su principal utilidad es el análisis del comportamiento de procesos estocásticos.

También se conoce como cadena simple biestable de Markov.


Según señaló Markov, en sistemas o procesos estocásticos (es decir, aleatorios) que presentan un estado presente es posible conocer sus antecedentes o desarrollo histórico. Por lo tanto, es factible establecer una descripción de la probabilidad futura de los mismos.

Más formalmente, la definición supone que en procesos estocásticos la probabilidad de que algo suceda solamente depende del pasado histórico de la realidad que estamos estudiando. Por este motivo, a menudo se dice que estas cadenas cuentan con memoria.

La base de las cadenas es la conocida como propiedad de Markov, la cual resume lo dicho anteriormente en la siguiente regla: lo que la cadena experimente en un momento t + 1 solamente depende de lo acontecido en el momento t (el inmediatamente anterior).

Dada esta sencilla explicación de la teoría, puede observarse que es posible a través de la misma conocer la probabilidad de que un estado ocurra en el largo plazo. Esto ayuda indudablemente a la predicción y estimación en largos periodos de tiempo.

¿Dónde se utiliza la cadena de Markov?

Las cadenas de Markov han experimentado una importante aplicación real en el ámbito de los negocios y las finanzas. Esto, al permitir, como se ha señalado, analizar y estimar futuros patrones de conducta de los individuos atendiendo a la experiencia y los resultados anteriores.

Lo anterior puede reflejarse en diferentes campos como la morosidad, el estudio de las conductas de consumidores, la demanda estacional de mano de obra, entre otros.

El sistema elaborado por Markov es bastante sencillo y cuenta, como hemos dicho, con una aplicación práctica bastante fácil. Sin embargo, muchas voces críticas señalan que un modelo tan simplificado no puede ser totalmente efectivo en procesos complejos.

Ejemplos:

  1. Una empresa esta considerando utilizar Cadenas de Markov para analizar los cambios en las preferencias de los usuarios por tres marcas distintas de un determinado producto. El estudio ha arrojado la siguiente estimación de la matriz de probabilidades de cambiarse de una marca a otra cada mes:


Si en la actualidad la participación de mercado es de 45%, 25% y 30%, respectivamente. ¿Cuales serán las participaciones de mercado de cada marca en dos meses más?.

En primer lugar definimos la variable aleatoria X_{n} que representa la marca que adquiere un cliente cualquiera en el mes n. Dicha variable aleatoria puede adoptar los valores 1,2,3 en el mes n=0,1,2,3,..

Adicionalmente conocemos cuál es la distribución inicial y la matriz de probabilidades de transición en una etapa tal como se observa a continuación:

distribucion-inicial-marcas

Luego para conocer la distribución de las participaciones de mercado al cabo de 2 meses (2 etapas) podemos utilizar la fórmula f^{n}=P^{T}*f^{n-1}:




Se concluye que las cuotas de mercado (participaciones de mercado) en dos meses a cambiado de un 45% a un 40.59%; de un 25% a un 33.91% y de un 30% a un 25.50%, para las marcas 1,2 y 3 respectivamente

Ejemplo No. 2
En una Unidad de Cuidados Intensivos en un determinado hospital, cada paciente es clasificado de acuerdo a un estado crítico, serio o estable. Estas clasificaciones son actualizadas cada mañana por un médico internista, de acuerdo a la evaluación experimentada por el paciente. Las probabilidades con las cuales cada paciente se mueve de un estado a otro se resumen en la tabla que sigue:


¿Cuál es la probabilidad que un paciente en estado crítico un día Jueves esté estable el día Sábado?.

Sea X_{n} la variable aleatoria que indica el estado que se encuentra un paciente cualquiera en el hospital en el día n. Los valores posibles para dicha variable son C, S y E, representando los estados crítico, serio y estable, respectivamente. Un grafo que representa dicho proceso estocástico dada la tabla anterior es:





La probabilidad de que un paciente esté en estado crítico el día Jueves y que el día Sábado esté estable, esta dado por: \mathbb{P}_{CE}^{2}, es decir, la probabilidad de pasar del estado crítico al estado estable al cabo de 2 etapas (días).

\mathbb{P}_{CE}^{2}=0,3*0,2+0,1*0,5+0,6*0,1=0,17

Notar que de forma equivalente se pueden utilizar las ecuaciones matriciales f^{n}=P^{T}*f^{n-1}:

ecuaciones-matriciales-hosp

Se comprueba que la probabilidad de pasar del estado crítico al estado estable al cabo de 2 etapas es de un 17%.

¿Cuál es la probabilidad que un paciente que está en estado estable el Lunes experimente alguna complicación y no esté estable nuevamente el Miércoles?.

En este caso cambia la distribución inicial respecto al escenario anterior (ahora el paciente está en estado estable), no obstante, también resulta de nuestro interés analizar qué sucede al cabo de 2 etapas.

transicion-hospital-markov

Con color verde se marca la probabilidad de que comenzando en un estado estable al cabo de 2 días un paciente se encuentre en estado crítico o serio. La suma de dichas probabilidades es un 66% que da respuesta a la interrogante anterior.

¿Qué porcentaje de la Unidad de Cuidados Intensivos usted diseñaría y equiparía para pacientes en estado crítico?.

Naturalmente se desea estimar la probabilidades de estado en el largo plazo independiente de la distribución inicial. La cadena es irreducible con estados recurrentes positivos aperiódicos. Utilizando las ecuaciones de estado estable presentadas en el Ejercicio N°2 se obtiene que \pi _{C}\cong0,2373, \pi _{S}\cong0,6184 y \pi _{E}\cong0,1443, que representan la probabilidad de que un individuo se encuentre en estado crítico, serio y estable, respectivamente.







en No hay comentarios:

lunes, 30 de mayo de 2022

 Distribuciones de probabilidades

Es el conjunto de valores distribuido de acuerdo con la teoría de las probabilidades y se consideran discretas cuando la variable aleatoria solo toma calores enteros 




Teorema del binomio

El álgebra es una rama de la matemática a través de la cual se pueden representar operaciones aritméticas utilizando números, letras y signos, y utilizando determinadas leyes y reglas para poder dar solución a cada una, según el respectivo caso. Una de las estructuras que comúnmente se estudian con el álgebra, son los binomios.

Este término dentro de la matemática, hace referencia a una expresión algebraica que tiene una estructura compuesta por dos términos o monomios. Cada uno de estos se encuentran identificados como los valores ubicados entre una sumo o una resta. Además, se construyen de distintas maneras: puede contener una variable y una constante, o también puede componerse de dos variables.


Ejemplo:

Expande el binomio {{(x+y)}^4} usando combinatorias.

Solución: Esto puede ser expandido de la siguiente manera:

=\left( {\begin{array}{*{20}{c}} 4 \\ 0 \end{array}} \right){{x}^{4}}+\left( {\begin{array}{*{20}{c}} 4 \\ 1 \end{array}} \right){{x}^{3}}y+\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right){{x}^{2}}{{y}^{2}} +\left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right)x{{y}^{3}}+\left( {\begin{array}{*{20}{c}} 4 \\ 4 \end{array}} \right){{y}^{4}}

Recordamos que tanto \left( {\begin{array}{*{20}{c}} 4 \\ 0 \end{array}} \right) como \left( {\begin{array}{*{20}{c}} 4 \\ 4 \end{array}} \right) son equivalentes a 1 ya que sólo hay una forma de escoger 0 y 4 elementos de un conjunto de 4 elementos. Entonces, tenemos: 

={{x}^{4}}+\left( {\begin{array}{*{20}{c}} 4 \\ 1 \end{array}} \right){{x}^{3}}y+\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right){{x}^{2}}{{y}^{2}} +\left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right)x{{y}^{3}}+{{y}^{4}}

Ahora evaluamos cada una de las combinatorias restantes:

\left( {\begin{array}{*{20}{c}} 4 \\ 1 \end{array}} \right)=\frac{{4!}}{{1!\left( {4-1} \right)!}}=\frac{{4!}}{{1!\left( 3 \right)!}}=4

\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right)=\frac{{4!}}{{2!\left( {4-2} \right)!}}=\frac{{4!}}{{2!\left( 2 \right)!}}=6

\left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right)=\frac{{4!}}{{3!\left( {4-3} \right)!}}=\frac{{4!}}{{3!\left( 1 \right)!}}=4

Al sustituir estos números en la expresión, tenemos: 

{{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}


2. Expande el binomio {{(x+y)}^5} usando el triángulo de Pascal.

Solución: Podemos observar que la fila 5 del triángulo de Pascal es 1, 5, 10, 10, 5, 1. Usando estos números para la expansión binomial, tenemos:

{{(x+y)}^5}={{x}^5}+5{{x}^4}y+10{{x}^3}{{y}^2} +10{{x}^2}{{y}^3}+5x{{y}^4}+{{y}^5}




Una distribución binomial es una distribución de probabilidad discreta que describe el número de éxitos al realizar n experimentos independientes entre sí, acerca de una variable aleatoria.

Existen una gran diversidad de experimentos o sucesos que pueden ser caracterizados bajo esta distribución de probabilidad. Imaginemos el lanzamiento de una moneda en el que definimos el suceso “sacar cara” como el éxito. Si lanzamos 5 veces la moneda y contamos los éxitos (sacar cara) que obtenemos, nuestra distribución de probabilidades se ajustaría a una distribución binomial.

Por lo tanto, la distribución binomial se entiende como una serie de pruebas o ensayos en la que solo podemos tener 2 resultados (éxito o fracaso), siendo el éxito nuestra variable aleatoria.

Propiedades de la distribución binomial

Para que una variable aleatoria se considere que sigue una distribución binomial, tiene que cumplir las siguientes propiedades:

  • En cada ensayo, experimento o prueba solo son posibles dos resultados (éxito o fracaso).
  • La probabilidad del éxito ha de ser constante. Esta se representa mediante la letra p. La probabilidad de que salga cara al lanzar una moneda es 0,5 y esta es constante dado que la moneda no cambia en cada experimento y las probabilidades de sacar cara son constantes.
  • La probabilidad de fracaso ha de ser también constate. Esta se representa mediante la letra q = 1-p. Es importante fijarse que mediante esa ecuación, sabiendo p o sabiendo q, podemos obtener la que nos falte.
  • El resultado obtenido en cada experimento es independiente del anterior. Por lo tanto, lo que ocurra en cada experimento no afecta a los siguientes.
  • Los sucesos son mutuamente excluyentes, es decir, no pueden ocurrir los 2 al mismo tiempo. No se puede ser hombre y mujer al mismo tiempo o que al lanzar una moneda salga cara y cruz al mismo tiempo.
  • Los sucesos son colectivamente exhaustivos, es decir, al menos uno de los 2 ha de ocurrir. Si no se es hombre, se es mujer y, si se lanza una moneda, si no sale cara ha de salir cruz.
  • La variable aleatoria que sigue una distribución binomial se suele representar como X~(n,p), donde n representa el número de ensayos o experimentos y p la probabilidad de éxito.

Formula de la distribución binomial

La fórmula para calcular la distribución normal es:

Donde:

n    = Número de ensayos/experimentos

x    = Número de éxitos

p    = Probabilidad de éxito

q    = Probabilidad de fracaso (1-p)

Es importante resaltar que la expresión entre corchetes no es una expresión matricial, sino que es un resultado de una combinatoria sin repetición. Este se obtiene con la siguiente formula:

El signo de exclamación en la expresión anterior representa el símbolo de factorial



Ejemplo:

1. Imaginemos que un 80% de personas en el mundo ha visto el partido de la final del último mundial de fútbol. Tras el evento, 4 amigos se reúnen a conversar, ¿Cuál es la probabilidad de que 3 de ellos hayan visto el partido?

Definamos las variables del experimento:

n    = 4 (es el total de la muestra que tenemos)

x    = número de éxitos, que en este caso es igual a 3, dado que buscamos la probabilidad de que 3 de los 4 amigos lo hayan visto.

p    = probabilidad de éxito (0,8)

q    = probabilidad de fracaso (0,2). Este resultado se obtiene al restar 1-p.

Tras definir todas nuestras variables, simplemente sustituimos en la formula.

El numerador del factorial se obtendría de multiplicar 4*3*2*1 = 24 y en el denominador tendríamos 3*2*1*1 = 6. Por lo tanto, el resultado del factorial sería 24/6=4.
Fuera del corchete tenemos dos números. El primero sería 0,8^3=0,512 y el segundo 0,2 (dado que 4-3 = 1 y cualquier número elevado a 1 es el mismo).

Por tanto, nuestro resultado final sería: 4*0,512*0,2 = 0,4096. Si multiplicamos por 100 tenemos que hay una probabilidad del 40,96% de que 3 de los 4 amigos haya visto el partido de la final del mundial.


Esperanza Matemática

La esperanza matemática de una variable aleatoria X, es el número que expresa el valor medio del fenómeno que representa dicha variable.

La esperanza matemática, también llamada valor esperado, es igual al sumatorio de las probabilidades de que exista un suceso aleatorio, multiplicado por el valor del suceso aleatorio. Dicho de otra forma, es el valor medio de un conjunto de datos. Esto, teniendo en cuenta que el término esperanza matemática está acuñado por la teoría de la probabilidad.

Mientras que en matemáticas, se denomina media matemática al valor promedio de un suceso que ha ocurrido. En distribuciones discretas con la misma probabilidad en cada suceso, la media aritmética es igual que la esperanza matemática.

Ejemplo: 

1. Imaginemos una moneda. Dos caras, cara y cruz. ¿Cual sería la esperanza matemática (valor esperado) de que salga cara?

Tiradas y resultado:

  1. Cara.
  2. Cruz.
  3. Cruz.
  4. Cara.
  5. Cruz.
  6. Cara.
  7. Cara.
  8. Cara.
  9. Cruz.
  10. Cruz.

¿Cuantas veces ha salido cara (contamos las C)? 5 veces ¿Cuantas veces ha salido cruz (contamos las X)? 5 veces. La probabilidad de que salga cara será de 5/10=0,5 o, en porcentaje, del 50%.

Una vez ha ocurrido ese suceso podemos calcular la media matemática del número de veces que ha ocurrido cada suceso. El lado cara ha salido una de cada dos veces, es decir, un 50% de las veces. La media coincide con la esperanza matemática.

Cálculo de la esperanza matemática

La esperanza matemática se calcula utilizando la probabilidad de cada suceso. La fórmula que formaliza este cálculo se enuncia como sigue:

Dónde:

  • X = valor del suceso.
  • P = Probabilidad de que ocurra.
  • i = Periodo en el que se da dicho suceso.
  • N = Número total de periodos u observaciones.

No siempre la probabilidad de que ocurra un suceso es la misma, como con las monedas. Existen infinidad de casos en que un suceso tiene más probabilidad de salir que otro. Por eso utilizamos en la fórmula la P. Además, al calcular números matemáticos debemos multiplicar por el valor del suceso. Abajo vemos un ejemplo.

¿Para qué se utiliza la esperanza matemática?

La esperanza matemática se utiliza en todas aquellas disciplinas en las que la presencia de sucesos probabilísticos es inherente a las mismas. Disciplinas tales como la estadística teórica, la física cuántica, la econometría, la biología o los mercados financieros. Una gran cantidad de procesos y sucesos que ocurren en el mundo son inexactos. Un ejemplo claro y fácil de entender es el de la bolsa de valores.

En la bolsa de valores, todo se calcula en base a valores esperados ¿Por qué valores esperados? Porque es lo que esperamos que suceda, pero no podemos confirmarlo. Todo se basa en probabilidades, no en certezas. Si el valor esperado o esperanza matemática de la rentabilidad de un activo es de un 10% anual, querrá decir que, según la información que tenemos del pasado, lo más probable es que la rentabilidad vuelva a ser de un 10%. Si solo tenemos en cuenta, claro está, la esperanza matemática como método para tomar nuestras decisiones de inversión.


En números, simplificando mucho, supongamos que las rentabilidades de un activo financiero son las siguientes:

Rentabilidad en los años 1, 2, 3 y 4.

  1. 12%.
  2. 6%.
  3. 15%
  4. 12%

El valor esperado sería el sumatorio de las rentabilidades multiplicadas por su probabilidad de suceder. La probabilidad de que «suceda» cada rentabilidad es de 0,25. Tenemos cuatro observaciones, cuatro años. Todos los años tienen la misma probabilidad de repetirse.

Esperanza = ( 12 x 0,25 ) + ( 6 x 0,25 ) + ( 15 x 0,25 ) + ( 12 x 0,25 ) = 3 + 1,5 + 3,75 + 3 = 11,25%

Teniendo en cuenta esta información, diremos que la esperanza de la rentabilidad del activo es del 11,25%.





en No hay comentarios:

sábado, 28 de mayo de 2022

DISTRIBUCION DE PROBABILIDADES

Probabilidad: posibilidad que suceda o no un determinado acontecimiento del cual se carece de información fidedigna o no se tiene certeza absoluta sobre su realización. Siempre se expresa en términos de que: “existe la probabilidad de que….” 

Matemáticamente, probabilidad es el coeficiente numérico que expresa la proporción en que un determinado acontecimiento puede ocurrir, en relación con un número de veces en que el experimento o fenómeno se realiza.

100% total probabilidad ==== 1 

0% nula probabilidad ==== 0  

La probabilidad siempre oscila entre 1 y 0 / entre 100 y 0

Probabilidad Clásica La probabilidad de que suceda o desarrolle un determinado suceso, se expresa matemáticamente por el cociente que resulta de dividir el número total de casos que son probables (favorables a que suceda) entre el número total de casos posibles. P(A)= Probabilidad de ocurrencia de un evento “A” h= número total de casos probables n=número total de casos posibles

Formula: 

P(A)= Probabilidad de ocurrencia de un evento "A"

h= numero total de casos probables

n= numero total de casos posibles



  • P(A) = 
    hn


Tenemos un mazo de 52 cartas de una baraja francesa, que consta de cuatro palos: corazones, tréboles, diamantes y picas. Entonces la probabilidad de extraer un corazón, sabiendo que hay 13 cartas de cada palo es:

  • P(A) = 
    hn

P (corazón) = 13/52= 52% 


en 2 comentarios:
Suscribirse a: Entradas (Atom)

 Arboles de Decisión Un árbol de decisión es una especie de mapa en que se muestra cada una de las opciones de decisión posibles y sus resul...

  • (sin título)
    PROGRAMACION LINEAL  La  Programación Lineal  (Optimización lineal), es el nombre que se le da al cálculo de la mejor solución, a un problem...
  • (sin título)
     Arboles de Decisión Un árbol de decisión es una especie de mapa en que se muestra cada una de las opciones de decisión posibles y sus resul...
  • (sin título)
     Distribuciones de probabilidades Es el conjunto de valores distribuido de acuerdo con la teoría de las probabilidades y se consideran discr...